MPG

Henry's Law Constants

www.henrys-law.org

Rolf Sander

Atmospheric Chemistry Division

Max-Planck Institute for Chemistry
Mainz, Germany

Home

Henry's Law Constants

Notes

References

Download

Errata

Contact, Imprint, Acknowledgements

When referring to the compilation of Henry's Law Constants, please cite this publication:

R. Sander: Compilation of Henry's law constants (version 5.0.0) for water as solvent, Atmos. Chem. Phys., 23, 10901-12440 (2023), doi:10.5194/acp-23-10901-2023

The publication from 2023 replaces that from 2015, which is now obsolete. Please do not cite the old paper anymore.

Henry's Law Constants → Organic species with oxygen (O) → Esters (RCOOR) → butyl methanoate

FORMULA:HCOOC4H9
TRIVIAL NAME: butyl formate
CAS RN:592-84-7
STRUCTURE
(FROM NIST):
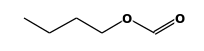
InChIKey:NMJJFJNHVMGPGM-UHFFFAOYSA-N

Hscp d ln Hs cp / d (1/T) References Type Notes
[mol/(m3Pa)] [K]
2.6×10−2 3700 Brockbank (2013) L
1.9×10−2 Plyasunov et al. (2004) L
1.9×10−2 Wittig et al. (2001) M
1.9×10−2 Duchowicz et al. (2020) V 187)
1.7×10−2 Yaws (2003) X 238) 404)
2.3×10−1 Duchowicz et al. (2020) Q
3.0×10−2 Wang et al. (2017) Q 81) 239)
2.1×10−2 Wang et al. (2017) Q 81) 240)
3.5×10−2 Wang et al. (2017) Q 81) 241)
1.4×10−2 Gharagheizi et al. (2012) Q
2.0×10−2 Raventos-Duran et al. (2010) Q 243) 244)
1.6×10−2 Raventos-Duran et al. (2010) Q 245)
1.6×10−2 Raventos-Duran et al. (2010) Q 246)
1.9×10−2 Gharagheizi et al. (2010) Q 247)
4.1×10−2 Modarresi et al. (2007) Q 68)
2.0×10−2 Yaffe et al. (2003) Q 249) 250)
3.5×10−2 Katritzky et al. (1998) Q
1.9×10−2 Yaws (1999) ? 21) 404)

Data

The first column contains Henry's law solubility constant Hscp at the reference temperature of 298.15 K.
The second column contains the temperature dependence d ln Hs cp / d (1/T), also at the reference temperature.

References

  • Brockbank, S. A.: Aqueous Henry’s law constants, infinite dilution activity coefficients, and water solubility: critically evaluated database, experimental analysis, and prediction methods, Ph.D. thesis, Brigham Young University, USA, URL https://scholarsarchive.byu.edu/etd/3691/ (2013).
  • Duchowicz, P. R., Aranda, J. F., Bacelo, D. E., & Fioressi, S. E.: QSPR study of the Henry’s law constant for heterogeneous compounds, Chem. Eng. Res. Des., 154, 115–121, doi:10.1016/J.CHERD.2019.12.009 (2020).
  • Gharagheizi, F., Abbasi, R., & Tirandazi, B.: Prediction of Henry’s law constant of organic compounds in water from a new group-contribution-based model, Ind. Eng. Chem. Res., 49, 10 149–10 152, doi:10.1021/IE101532E (2010).
  • Gharagheizi, F., Eslamimanesh, A., Mohammadi, A. H., & Richon, D.: Empirical method for estimation of Henry’s law constant of non-electrolyte organic compounds in water, J. Chem. Thermodyn., 47, 295–299, doi:10.1016/J.JCT.2011.11.015 (2012).
  • Katritzky, A. R., Wang, Y., Sild, S., Tamm, T., & Karelson, M.: QSPR studies on vapor pressure, aqueous solubility, and the prediction of water-air partition coefficients, J. Chem. Inf. Comput. Sci., 38, 720–725, doi:10.1021/CI980022T (1998).
  • Modarresi, H., Modarress, H., & Dearden, J. C.: QSPR model of Henry’s law constant for a diverse set of organic chemicals based on genetic algorithm-radial basis function network approach, Chemosphere, 66, 2067–2076, doi:10.1016/J.CHEMOSPHERE.2006.09.049 (2007).
  • Plyasunov, A. V., Plyasunova, N. V., & Shock, E. L.: Group contribution values for the thermodynamic functions of hydration of aliphatic esters at 298.15 K, 0.1 MPa, J. Chem. Eng. Data, 49, 1152–1167, doi:10.1021/JE049850A (2004).
  • Raventos-Duran, T., Camredon, M., Valorso, R., Mouchel-Vallon, C., & Aumont, B.: Structure-activity relationships to estimate the effective Henry’s law constants of organics of atmospheric interest, Atmos. Chem. Phys., 10, 7643–7654, doi:10.5194/ACP-10-7643-2010 (2010).
  • Wang, C., Yuan, T., Wood, S. A., Goss, K.-U., Li, J., Ying, Q., & Wania, F.: Uncertain Henry’s law constants compromise equilibrium partitioning calculations of atmospheric oxidation products, Atmos. Chem. Phys., 17, 7529–7540, doi:10.5194/ACP-17-7529-2017 (2017).
  • Wittig, R., Lohmann, J., Joh, R., Horstmann, S., & Gmehling, J.: Vapor-liquid equilibria and enthalpies of mixing in a temperature range from 298.15 to 413.15K for the further development of modified UNIFAC (Dortmund), Ind. Eng. Chem. Res., 40, 5831–5838, doi:10.1021/IE010444J (2001).
  • Yaffe, D., Cohen, Y., Espinosa, G., Arenas, A., & Giralt, F.: A fuzzy ARTMAP-based quantitative structure-property relationship (QSPR) for the Henry’s law constant of organic compounds, J. Chem. Inf. Comput. Sci., 43, 85–112, doi:10.1021/CI025561J (2003).
  • Yaws, C. L.: Chemical Properties Handbook, McGraw-Hill, Inc., ISBN 0070734011 (1999).
  • Yaws, C. L.: Yaws’ Handbook of Thermodynamic and Physical Properties of Chemical Compounds, Knovel: Norwich, NY, USA, ISBN 1591244447 (2003).

Type

Table entries are sorted according to reliability of the data, listing the most reliable type first: L) literature review, M) measured, V) VP/AS = vapor pressure/aqueous solubility, R) recalculation, T) thermodynamical calculation, X) original paper not available, C) citation, Q) QSPR, E) estimate, ?) unknown, W) wrong. See Section 3.1 of Sander (2023) for further details.

Notes

21) Several references are given in the list of Henry's law constants but not assigned to specific species.
68) Modarresi et al. (2007) use different descriptors for their calculations. They conclude that a genetic algorithm/radial basis function network (GA/RBFN) is the best QSPR model. Only these results are shown here.
81) Value at T = 288 K.
187) Estimation based on the quotient between vapor pressure and water solubility, extracted from HENRYWIN.
238) Value given here as quoted by Gharagheizi et al. (2010).
239) Calculated using linear free energy relationships (LFERs).
240) Calculated using SPARC Performs Automated Reasoning in Chemistry (SPARC).
241) Calculated using COSMOtherm.
243) Value from the training dataset.
244) Calculated using the GROMHE model.
245) Calculated using the SPARC approach.
246) Calculated using the HENRYWIN method.
247) Calculated using a combination of a group contribution method and neural networks.
249) Yaffe et al. (2003) present QSPR results calculated with the fuzzy ARTMAP (FAM) and with the back-propagation (BK-Pr) method. They conclude that FAM is better. Only the FAM results are shown here.
250) Value from the training set.
404) Value at T = 300 K.

The numbers of the notes are the same as in Sander (2023). References cited in the notes can be found here.

* * *

Search Henry's Law Database

Species Search:
Identifier Search:
Reference Search:

* * *

Convert Henry's Law Constants

Convert:

* * *