MPG

Henry's Law Constants

www.henrys-law.org

Rolf Sander

Atmospheric Chemistry Division

Max-Planck Institute for Chemistry
Mainz, Germany

Home

Henry's Law Constants

Notes

References

Download

Errata

Contact, Imprint, Acknowledgements

When referring to the compilation of Henry's Law Constants, please cite this publication:

R. Sander: Compilation of Henry's law constants (version 5.0.0) for water as solvent, Atmos. Chem. Phys., 23, 10901-12440 (2023), doi:10.5194/acp-23-10901-2023

The publication from 2023 replaces that from 2015, which is now obsolete. Please do not cite the old paper anymore.

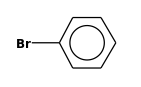
Henry's Law Constants → Organic species with bromine (Br) → Bromocarbons (C, H, O, N, Br) → bromobenzene

FORMULA:C6H5Br
CAS RN:108-86-1
STRUCTURE
(FROM NIST):
InChIKey:QARVLSVVCXYDNA-UHFFFAOYSA-N

Hscp d ln Hs cp / d (1/T) References Type Notes
[mol/(m3Pa)] [K]
4.3×10−3 4500 Brockbank (2013) L 1)
5.0×10−3 4200 Fogg and Sangster (2003) L
4.8×10−3 Mackay and Shiu (1981) L
6.0×10−3 4300 Hiatt (2013) M
3.9×10−3 2900 Lau et al. (2010) M 11)
5.0×10−3 de Wolf and Lieder (1998) M 88)
4.0×10−3 Shiu and Mackay (1997) M
6.1×10−3 Hovorka and Dohnal (1997) M 12)
4.9×10−3 4200 Kondoh and Nakajima (1997) M
5.3×10−3 5300 Hansen et al. (1993) M 282)
4.4×10−3 Li and Carr (1993) M
4.0×10−3 Mackay and Shiu (1981) M
4.7×10−3 Shiu and Mackay (1997) V
4.7×10−3 Mackay et al. (1993) V
5.0×10−3 Hwang et al. (1992) V
4.7×10−3 Hine and Mookerjee (1975) V
4.6×10−3 Yaws (2003) X 238)
4.7×10−3 HSDB (2015) C
4.0×10−3 Schüürmann (2000) C 21)
7.4×10−3 Keshavarz et al. (2022) Q
7.9×10−3 Duchowicz et al. (2020) Q 185)
3.1×10−2 Gharagheizi et al. (2012) Q
6.2×10−3 Raventos-Duran et al. (2010) Q 243) 244)
6.2×10−3 Raventos-Duran et al. (2010) Q 245)
4.9×10−3 Raventos-Duran et al. (2010) Q 246)
4.2×10−3 Gharagheizi et al. (2010) Q 247)
5.2×10−3 Hilal et al. (2008) Q
7.7×10−3 Modarresi et al. (2007) Q 68)
4800 Kühne et al. (2005) Q
4.1×10−3 Yaffe et al. (2003) Q 249) 250)
4.2×10−3 Yao et al. (2002) Q 230)
5.4×10−3 English and Carroll (2001) Q 231) 232)
2.9×10−3 Katritzky et al. (1998) Q
5.1×10−3 Suzuki et al. (1992) Q 233)
7.3×10−3 Nirmalakhandan and Speece (1988) Q
4.0×10−3 Duchowicz et al. (2020) ? 21) 186)
4300 Kühne et al. (2005) ?
4.6×10−3 Yaws (1999) ? 21)
4.7×10−3 Yaws and Yang (1992) ? 21)
4.7×10−3 Abraham et al. (1990) ?

Data

The first column contains Henry's law solubility constant Hscp at the reference temperature of 298.15 K.
The second column contains the temperature dependence d ln Hs cp / d (1/T), also at the reference temperature.

References

  • Abraham, M. H., Whiting, G. S., Fuchs, R., & Chambers, E. J.: Thermodynamics of solute transfer from water to hexadecane, J. Chem. Soc. Perkin Trans. 2, pp. 291–300, doi:10.1039/P29900000291 (1990).
  • Brockbank, S. A.: Aqueous Henry’s law constants, infinite dilution activity coefficients, and water solubility: critically evaluated database, experimental analysis, and prediction methods, Ph.D. thesis, Brigham Young University, USA, URL https://scholarsarchive.byu.edu/etd/3691/ (2013).
  • de Wolf, W. & Lieder, P. H.: A novel method to determine uptake and elimination kinetics of volatile chemicals in fish, Chemosphere, 36, 1713–1724, doi:10.1016/S0045-6535(97)10062-5 (1998).
  • Duchowicz, P. R., Aranda, J. F., Bacelo, D. E., & Fioressi, S. E.: QSPR study of the Henry’s law constant for heterogeneous compounds, Chem. Eng. Res. Des., 154, 115–121, doi:10.1016/J.CHERD.2019.12.009 (2020).
  • English, N. J. & Carroll, D. G.: Prediction of Henry’s law constants by a quantitative structure property relationship and neural networks, J. Chem. Inf. Comput. Sci., 41, 1150–1161, doi:10.1021/CI010361D (2001).
  • Fogg, P. & Sangster, J.: Chemicals in the Atmosphere: Solubility, Sources and Reactivity, John Wiley & Sons, Inc., ISBN 978-0-471-98651-5 (2003).
  • Gharagheizi, F., Abbasi, R., & Tirandazi, B.: Prediction of Henry’s law constant of organic compounds in water from a new group-contribution-based model, Ind. Eng. Chem. Res., 49, 10 149–10 152, doi:10.1021/IE101532E (2010).
  • Gharagheizi, F., Eslamimanesh, A., Mohammadi, A. H., & Richon, D.: Empirical method for estimation of Henry’s law constant of non-electrolyte organic compounds in water, J. Chem. Thermodyn., 47, 295–299, doi:10.1016/J.JCT.2011.11.015 (2012).
  • Hansen, K. C., Zhou, Z., Yaws, C. L., & Aminabhavi, T. M.: Determination of Henry’s law constants of organics in dilute aqueous solutions, J. Chem. Eng. Data, 38, 546–550, doi:10.1021/JE00012A017 (1993).
  • Hiatt, M. H.: Determination of Henry’s law constants using internal standards with benchmark values, J. Chem. Eng. Data, 58, 902–908, doi:10.1021/JE3010535 (2013).
  • Hilal, S. H., Ayyampalayam, S. N., & Carreira, L. A.: Air-liquid partition coefficient for a diverse set of organic compounds: Henry’s law constant in water and hexadecane, Environ. Sci. Technol., 42, 9231–9236, doi:10.1021/ES8005783 (2008).
  • Hine, J. & Mookerjee, P. K.: The intrinsic hydrophilic character of organic compounds. Correlations in terms of structural contributions, J. Org. Chem., 40, 292–298, doi:10.1021/JO00891A006 (1975).
  • Hovorka, Š. & Dohnal, V.: Determination of air–water partitioning of volatile halogenated hydrocarbons by the inert gas stripping method, J. Chem. Eng. Data, 42, 924–933, doi:10.1021/JE970046G (1997).
  • HSDB: Hazardous Substances Data Bank, TOXicology data NETwork (TOXNET), National Library of Medicine (US), URL https://www.nlm.nih.gov/toxnet/Accessing_HSDB_Content_from_PubChem.html (2015).
  • Hwang, Y.-L., Olson, J. D., & Keller, II, G. E.: Steam stripping for removal of organic pollutants from water. 2. Vapor-liquid equilibrium data, Ind. Eng. Chem. Res., 31, 1759–1768, doi:10.1021/IE00007A022 (1992).
  • Katritzky, A. R., Wang, Y., Sild, S., Tamm, T., & Karelson, M.: QSPR studies on vapor pressure, aqueous solubility, and the prediction of water-air partition coefficients, J. Chem. Inf. Comput. Sci., 38, 720–725, doi:10.1021/CI980022T (1998).
  • Keshavarz, M. H., Rezaei, M., & Hosseini, S. H.: A simple approach for prediction of Henry’s law constant of pesticides, solvents, aromatic hydrocarbons, and persistent pollutants without using complex computer codes and descriptors, Process Saf. Environ. Prot., 162, 867–877, doi:10.1016/J.PSEP.2022.04.045 (2022).
  • Kondoh, H. & Nakajima, T.: Optimization of headspace cryofocus gas chromatography/mass spectrometry for the analysis of 54 volatile organic compounds, and the measurement of their Henry’s constants, J. Environ. Chem., 7, 81–89, doi:10.5985/JEC.7.81 (1997).
  • Kühne, R., Ebert, R.-U., & Schüürmann, G.: Prediction of the temperature dependency of Henry’s law constant from chemical structure, Environ. Sci. Technol., 39, 6705–6711, doi:10.1021/ES050527H (2005).
  • Lau, K., Rogers, T. N., & Chesney, D. J.: Measuring the aqueous Henry’s law constant at elevated temperatures using an extended EPICS technique, J. Chem. Eng. Data, 55, 5144–5148, doi:10.1021/JE100701W (2010).
  • Li, J. & Carr, P. W.: Measurement of water-hexadecane partition coefficients by headspace gas chromatography and calculation of limiting activity coefficients in water, Anal. Chem., 65, 1443–1450, doi:10.1021/AC00058A023 (1993).
  • Mackay, D. & Shiu, W. Y.: A critical review of Henry’s law constants for chemicals of environmental interest, J. Phys. Chem. Ref. Data, 10, 1175–1199, doi:10.1063/1.555654 (1981).
  • Mackay, D., Shiu, W. Y., & Ma, K. C.: Illustrated Handbook of Physical-Chemical Properties and Environmental Fate for Organic Chemicals, vol. III of Volatile Organic Chemicals, Lewis Publishers, Boca Raton, ISBN 0873719735 (1993).
  • Modarresi, H., Modarress, H., & Dearden, J. C.: QSPR model of Henry’s law constant for a diverse set of organic chemicals based on genetic algorithm-radial basis function network approach, Chemosphere, 66, 2067–2076, doi:10.1016/J.CHEMOSPHERE.2006.09.049 (2007).
  • Nirmalakhandan, N. N. & Speece, R. E.: QSAR model for predicting Henry’s constant, Environ. Sci. Technol., 22, 1349–1357, doi:10.1021/ES00176A016 (1988).
  • Raventos-Duran, T., Camredon, M., Valorso, R., Mouchel-Vallon, C., & Aumont, B.: Structure-activity relationships to estimate the effective Henry’s law constants of organics of atmospheric interest, Atmos. Chem. Phys., 10, 7643–7654, doi:10.5194/ACP-10-7643-2010 (2010).
  • Schüürmann, G.: Prediction of Henry’s law constant of benzene derivatives using quantum chemical continuum-solvation models, J. Comput. Chem., 21, 17–34, doi:10.1002/(SICI)1096-987X(20000115)21:1<17::AID-JCC3>3.0.CO;2-5 (2000).
  • Shiu, W.-Y. & Mackay, D.: Henry’s law constants of selected aromatic hydrocarbons, alcohols, and ketones, J. Chem. Eng. Data, 42, 27–30, doi:10.1021/JE960218U (1997).
  • Suzuki, T., Ohtaguchi, K., & Koide, K.: Application of principal components analysis to calculate Henry’s constant from molecular structure, Comput. Chem., 16, 41–52, doi:10.1016/0097-8485(92)85007-L (1992).
  • Yaffe, D., Cohen, Y., Espinosa, G., Arenas, A., & Giralt, F.: A fuzzy ARTMAP-based quantitative structure-property relationship (QSPR) for the Henry’s law constant of organic compounds, J. Chem. Inf. Comput. Sci., 43, 85–112, doi:10.1021/CI025561J (2003).
  • Yao, X., aand X. Zhang, M. L., Hu, Z., & Fan, B.: Radial basis function network-based quantitative structure-property relationship for the prediction of Henry’s law constant, Anal. Chim. Acta, 462, 101–117, doi:10.1016/S0003-2670(02)00273-8 (2002).
  • Yaws, C. L.: Chemical Properties Handbook, McGraw-Hill, Inc., ISBN 0070734011 (1999).
  • Yaws, C. L.: Yaws’ Handbook of Thermodynamic and Physical Properties of Chemical Compounds, Knovel: Norwich, NY, USA, ISBN 1591244447 (2003).
  • Yaws, C. L. & Yang, H.-C.: Henry’s law constant for compound in water, in: Thermodynamic and Physical Property Data, edited by Yaws, C. L., pp. 181–206, Gulf Publishing Company, Houston, TX, ISBN 0884150313 (1992).

Type

Table entries are sorted according to reliability of the data, listing the most reliable type first: L) literature review, M) measured, V) VP/AS = vapor pressure/aqueous solubility, R) recalculation, T) thermodynamical calculation, X) original paper not available, C) citation, Q) QSPR, E) estimate, ?) unknown, W) wrong. See Section 3.1 of Sander (2023) for further details.

Notes

1) A detailed temperature dependence with more than one parameter is available in the original publication. Here, only the temperature dependence at 298.15 K according to the van 't Hoff equation is presented.
11) Measured at high temperature and extrapolated to T⊖ = 298.15 K.
12) Value at T = 293 K.
21) Several references are given in the list of Henry's law constants but not assigned to specific species.
68) Modarresi et al. (2007) use different descriptors for their calculations. They conclude that a genetic algorithm/radial basis function network (GA/RBFN) is the best QSPR model. Only these results are shown here.
88) Value at T = 295 K.
185) Value from the validation set for checking whether the model is satisfactory for compounds that are absent from the training set.
186) Experimental value, extracted from HENRYWIN.
230) Yao et al. (2002) compared two QSPR methods and found that radial basis function networks (RBFNs) are better than multiple linear regression. In their paper, they provide neither a definition nor the unit of their Henry's law constants. Comparing the values with those that they cite from Yaws (1999), it is assumed that they use the variant Hvpx and the unit atm.
231) English and Carroll (2001) provide several calculations. Here, the preferred value with explicit inclusion of hydrogen bonding parameters from a neural network is shown.
232) Value from the training dataset.
233) Calculated with a principal component analysis (PCA); see Suzuki et al. (1992) for details.
238) Value given here as quoted by Gharagheizi et al. (2010).
243) Value from the training dataset.
244) Calculated using the GROMHE model.
245) Calculated using the SPARC approach.
246) Calculated using the HENRYWIN method.
247) Calculated using a combination of a group contribution method and neural networks.
249) Yaffe et al. (2003) present QSPR results calculated with the fuzzy ARTMAP (FAM) and with the back-propagation (BK-Pr) method. They conclude that FAM is better. Only the FAM results are shown here.
250) Value from the training set.
282) The same data were also published in Hansen et al. (1995).

The numbers of the notes are the same as in Sander (2023). References cited in the notes can be found here.

* * *

Search Henry's Law Database

Species Search:
Identifier Search:
Reference Search:

* * *

Convert Henry's Law Constants

Convert:

* * *